TG-21: Historic Linac Dosimetry
Downloads
AAPM TG-21: A protocol for the determination of absorbed dose from high-energy photon and electron beams (External link)
Overview
Released in 1983, TG-21 sought to standardize the calibration of absorbed dose for high energy photon and electron fields. TG-21 is the predecessor to TG-51 and the TG-51 Addendum which have superseded it in clinical practice in the US. Although TG-51 greatly simplified the calibration of clinical photon and electron beams, it does so by hiding much of the physics that TG-21 explicitly states. Thus understanding the TG-21 methodology is critical to understanding current calibration standard of practice for clinical beams.
TG-21 Simplified Procedure
- The ion chamber to be used is calibrated by an Accredited Dosimetry Calibration Laboratory (ADCL). The ADCL may return a cavity-gas calibration factor, \(N_{gas}\), for use in the protocol or an exposure calibration factor, \(N_X\), which may be converted to \(N_{gas}\) by the site physicist. \(N_{gas}\) is defined simply as in the below equation where \(D_{gas}\) is the dose to chamber fill gas, \(A_{ion}\) is the ionization collection efficiency during calibration at the ADCL, and \(M\) is the electrometer measurement. \begin{equation} \label{eq:N_gas} N_{gas}= \frac{D_{gas} A_{ion}}{M} \end{equation}
- Measurement, \(M\), is made in a phantom made of either water, acrylic, or polystyrene. The product of this measurement and the cavity-gas calibration factor is the dose to gas in the chamber at the point of measurement. \(P_{ion}\) corrects for collection electron collection inefficiency during measurement. \begin{equation} \label{eq:D_gas} D_{gas} = MN_{gas}P_{ion} \end{equation}
- Dose to the phantom material at the point of measurement (in absence of ion chamber) is obtained by the product of the dose to gas and the ratio of stopping powers from air to the medium, \((\frac{\overline{L}}{\rho})_{gas}^{med}\). \(P_{repl}\) and \(P_{wall}\) correct for ion chamber influences on the dose distribution. As per Bragg-Gray Cavity Theory, this step requires measurement of beam quality to accurately asses ratio of stopping powers between air and the medium. Stopping power for a material is dependent upon the photon energy. \begin{equation} \label{eq:D_med simple} D_{med} = D_{gas} (\frac{\overline{L}}{\rho})_{gas}^{med} P_{repl}P_{wall} \end{equation}
- Dose to water is obtained as the product of dose to the phantom medium by the ratio of mass energy-absorption coefficients between water and the medium. This measurement is taken in the exponentially decreasing portion of the percent depth dose (%DD) curve for photons and at depth of maximum dose (\(d_{max}\)) for electrons. Excess scatter correction (ESC) and electron fluence correction (\(\phi_{med}^{water}\)) correct for phantom effects on fluence relative to water. More detail on these terms is given below. \begin{equation} \label{eq: D_Water photon} D_{water} = D_{med} \times ESC \times (\frac{\overline \mu}{\rho})_{med}^{water} \quad \textrm{for photon fields} \end{equation} \begin{equation} \label{eq:D_Water electron} D_{water} = D_{med} \times \phi_{med}^{water} \times (\frac{\overline L}{\rho})_{med}^{water} \quad \textrm{for electron fields} \end{equation}
- For photons, the dose at reference depth is scaled using %DD to \(d_{max}\).
Important Points
Phantoms
TG-21 allowed reference measurements to be made in Acrylic or Polystyrene phantoms as well as water.
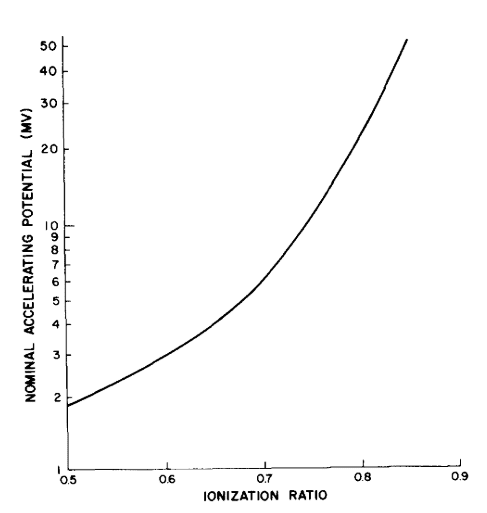
Beam Quality (Nominal Accelerating Potential and Mean Incident Energy)
Determination of stopping powers in BG cavity theory requires knowledge of the beam quality. Beam quality is specified as Nominal Ionizing Potential for photon beam and Mean Incident Energy for electron beams.
Nominal Ionizing Potential is determined by computing the ratio of measurement at a depth of 10cm to a depth of 20cm with an SSD of 100cm in a 10x10\(cm^2\) field of water. This measurement can be made in polystyrene or acrylic phantoms, in which case the depth of overlying material is decreased and the SSD is increased such that the source to detector distance (SDD) remains unchanged.
\begin{equation} \label{eq:ionization ratio} \textrm{Ionization Ratio} = \frac{M_{SDD = 10cm}}{M_{SDD = 120cm }} \end{equation}
Mean Incident Energy is determined by the below equation where \(d_{50}\) is the depth in water in which the ion chamber reading is 50% of its maximum reading, and \(f\) is a scaling factor with a value of 0.965, 1, or 1.11 for polystyrene, water, or acrylic respectively. It is recommended that \(d_50\) be measured in a large enough field size that further increasing the field size does not influence depth of maximum dose.
\begin{equation} \label{eq: mean incident energy} \bar{E}_0 = 2.33 \times d_{50} \times f \end{equation}
Depth of Calibration
For photon beams the depth of calibration is dependent upon the depth of maximum dose \(d_{max}\) and the ion chamber inner diameter but is taken in the exponentially decreasing portion of the percent dept dose (%DD) curve. Increasing portions of the %DD curve should not be used because CPE is not established. Depth of maximum dose is not an optimal position because \(P_{repl}\) is not well quantified in this region.
Electron beams should be calibrated at \(d_{max}\).
Gas Cavity Calibration Factor \({N_{gas}}\)
Ngas is a factor unique to each ionization chamber that is related to the volume of the chamber, where \( (\frac{\bar{W}}{e}) = 33.97 \frac{J}{C}\) and \( \rho_{air} = 1.2 \frac{kg}{m^3} \).
\begin{equation} \label{eq: N_gas definition} N_{gas} = \frac{(\frac{\bar{W}}{e})}{\rho_{air}V_{chamber}} = \frac{2.83 \times 10^7}{V_c (cm^3)} GyC^{-1} \end{equation}
The historical primary measurement made at an ADCL was Exposure, \(X\) and so it is useful to understand how \(N_{gas}\) may be obtained from the exposure calibration factor \(N_x\).
\begin{equation} \label{eq: N_X} N_x = \frac {X}{M} \end{equation}
Ignoring corrections conversions for the chamber itself, \(N_{gas}\) may be computed as:
\begin{equation} \label{eq:N_gas from X} N_{gas} = \frac{D_{gas} N_x A_{ion}}{X} \end{equation}
\(D_{gas}\) and \(X\) may be removed by noting that, under charged particle equilibrium (CPE), they are related by the below equation where \(k\) is a conversion factor equal to \(2.58 \times 10 ^{-4}\frac{C}{kg \ R}\) and \(\frac{W}{e}= 33.97 \frac{J}{C}\) is the mean energy required to ionize air.
\begin{equation} \label{eq: D_gas and X} D_{gas} = X k (\frac{W}{e}) \end{equation}
This yields the simplified conversion equation given below. The full conversion equation, which includes factors accounting for fluence perturbation by the ion chamber materials, is given as equation 5 in TG-21.
\begin{equation} \label{eq: N_gas conversion simple} N_{gas} = N_x k (\frac{W}{e}) A_{ion} \end{equation}
Normalized Ion Chamber Measurement (M)
TG-21 corrects the measurement only to standard temperature and pressure. This corrects for the difference in mass of air between current conditions and the conditions for which \(N_{gas}\) was provided. Note that this is slightly difference from TG-51 which also corrects for chamber collection inefficiency, polarity effects, and electrometer efficiency.
\begin{equation} \label{eq: TP correction} M = M_{raw} \frac{T + 273^\circ C}{295 ^\circ C} \times \frac{760mmHg}{P} \end{equation}
Navigation
Not a Premium Member?
Sign up today to get access to hundreds of ABR style practice questions.
