Interactions of Ionizing Radiation
Photon Interactions
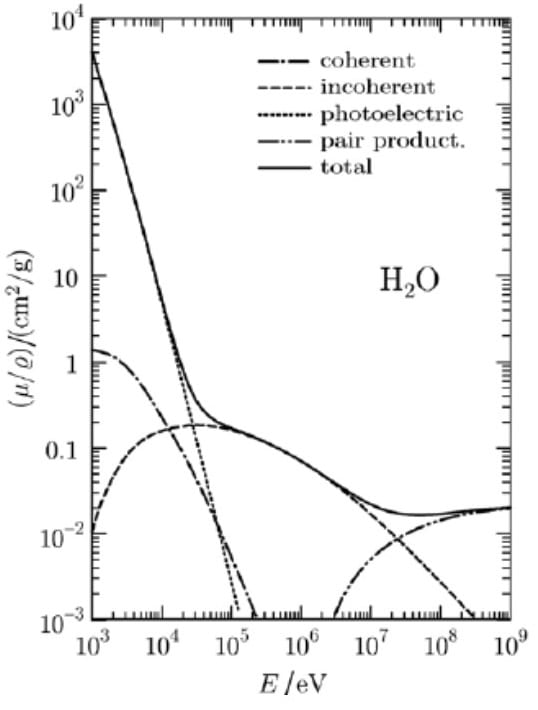
There are 4 main interactions between photons (X-rays and gamma rays) and matter. These are coherent scattering, photoelectric absorption, Compton scattering, and pair production.
Several factors impact the probability that a photon will undergo an interaction with matter including the energy of the photon and the properties of the atoms making up the material, largely driven by the atomic number (Z) of the absorber.
Coherent Scattering
Coherent scattering occurs when a photon undergoes an elastic scattering event with a material. Because the scattering is elastic no energy is lost by the photon during the interaction.
Important Points
- Primarily for low energy photons
- Two types of coherent scattering
- Rayleigh Scattering
- Elastic scattering of light by all electrons in the atom
- Thomson scattering
- Elastic scattering of light by a single electron in the atom
- Rayleigh Scattering
Probability of Coherent Scattering
![]()
Photoelectric Absorption
The photoelectric effect occurs when a photon is absorbed by an inner shell electron causing the electron to gain sufficient energy to be ejected from the atom.
After ejection of the inner shell electron, the missing electron must be replaced by an outer shell (higher energy) electron. For this to happen, the outer shell electrons must lose energy by emission of a characteristic X-ray and/or an Auger Electron.
Requirements
- Energy threshold (minimum required energy) equal to the binding energy of the orbital electron
Energy After Interaction
![]()
Probability of Photoelectric Absorption
![]()
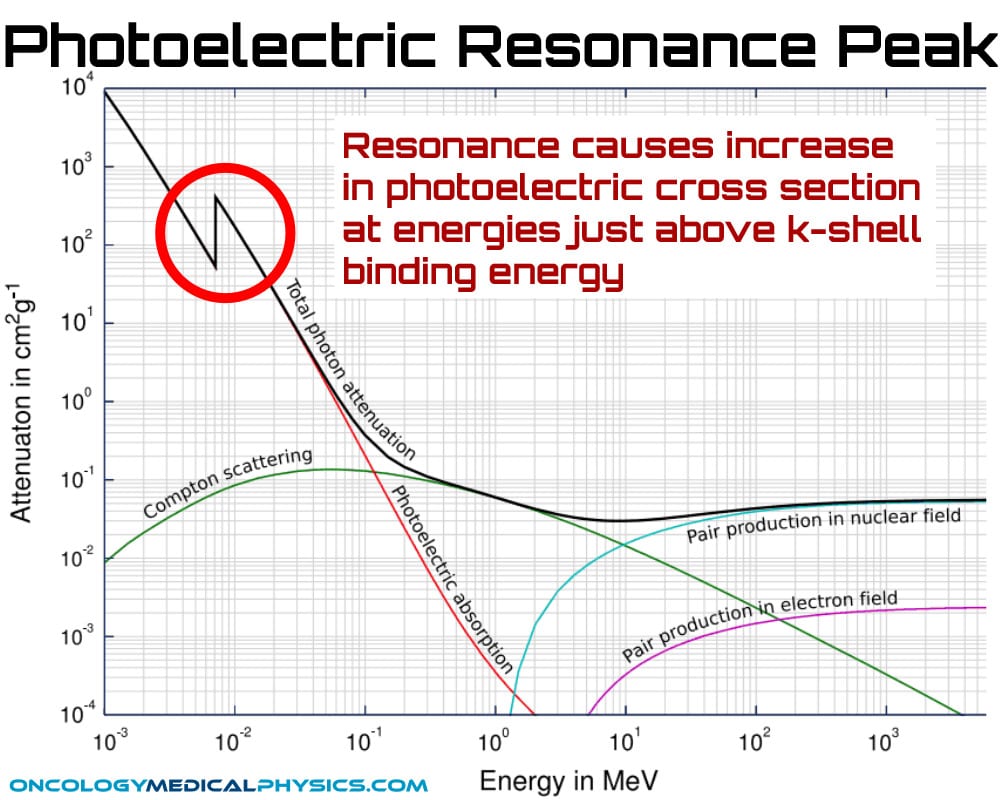
Resonance: The photoelectric effect exhibits a resonance phenomenon in which photons with energy close to the binding energy of an electron greatly increase the probability of interaction.
- Resonance peaks are named for their electron shells (i.e. k-edge)
- These peaks are exploited for use in imaging contrast in CT.
Characteristic X-rays
Characteristic X-rays are emitted as atomic outer-shell electron decay to a lower energy state.
Called “characteristic” because their energy is tied to the quantized energy levels between atomic orbitals causing the X-ray spectrum to be unique to a given element.
![]()
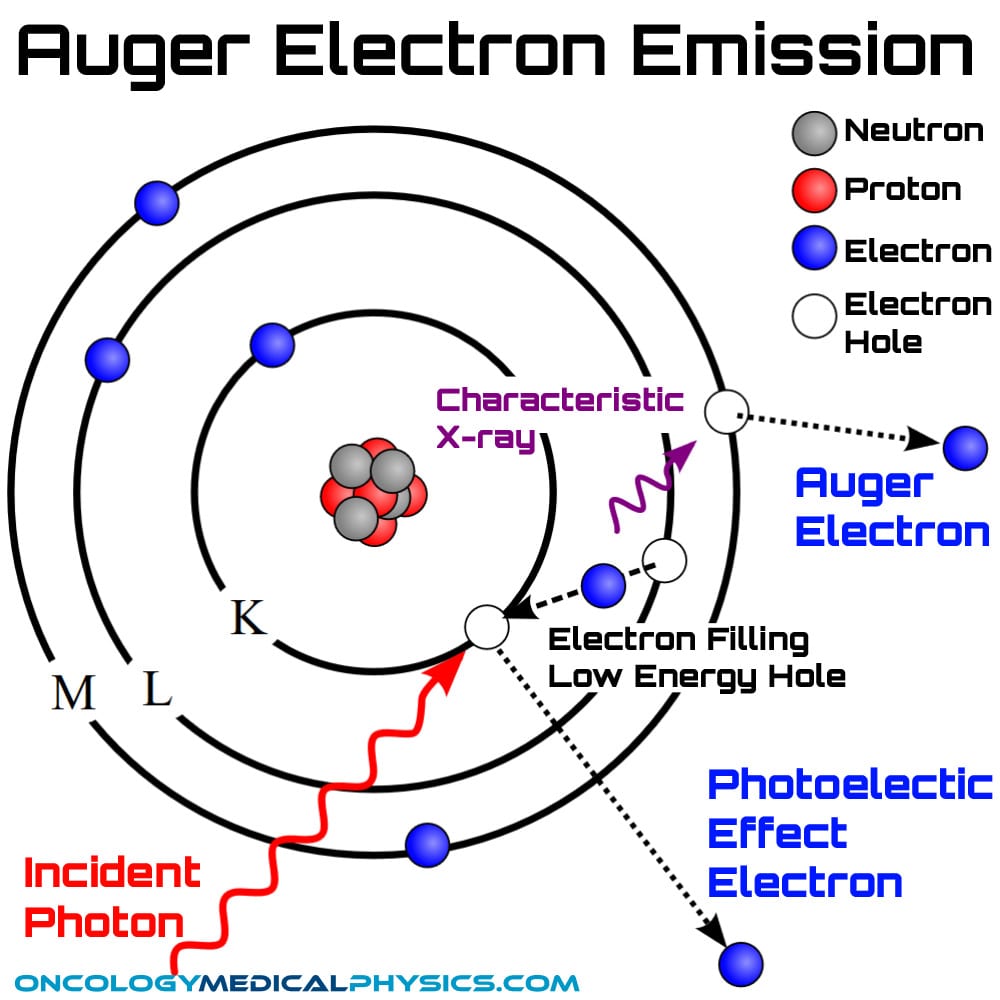
Auger Electrons
Auger electron emission is a competing means by which an atomic orbital may lose energy to fill a lower energy electron hole with a higher energy electron via the emission of another electron.
Auger electron emission may be thought of as a two-step process:
- A higher energy electron emits a characteristic X-ray, thereby losing sufficient energy to fill the hole.
- The characteristic X-ray is absorbed by another electron which is then ejected from the atom. This is the Auger electron.
![]()
- EAuger Electron is the kinetic energy of the Auger electron
- ΔEAtomic State is the difference in energy between the initial and final atomic state
- EBinding is the binding energy of the Auger Electron prior to ejection
Compton Scattering
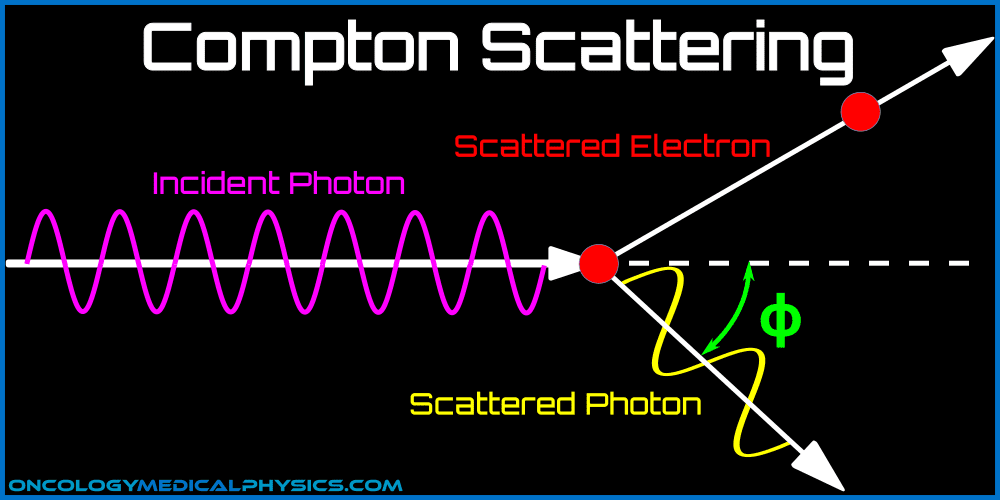
Compton scattering is an inelastic scattering event in which the incident photon interacts with a single electron. Because the interaction is inelastic, the photon transfers some of its energy to the electron during the interaction. This causes the electron to be ejected from its orbital.
Compton scattering is the most probable photon interaction in water for photons in the range of about 30keV to 24MeV.
Key Point: Because the Compton dominant range in soft tissue extends from 30keV to 24MeV, Compton scattering is a very important interaction of medical applications both in imaging and for radiation therapy!
Probability of Compton Scattering
![]()
Because Compton scattering involves interaction of a photon with a single electron, the electron density (number of electrons per unit mass) is the most important material property for Compton scattering interaction cross section.
Hydrogen has no neutrons and, therefore, about double the electron density of other atoms. This means that hydrogen has about double the Compton interactions per unit mass than any other low mass element.
For light elements other than hydrogen, the electron density is roughly constant. As a result, the probability of Compton scattering is nearly independent of effective atomic number.
| Element/Material | Density (g/cc) | Effective Atomic Number | Electrons per gram |
| Hydrogen | 0.0009 | 1 | 6 × 1023 |
| Carbon | 2.25 | 6 | 3.01 × 1023 |
| Lead | 11.3 | 82 | 2.38 × 1023 |
| Air | 0.00129 | 7.64 | 3.01 × 1023 |
| Water | 1.0 | 7.42 | 3.34 × 1023 |
| Fat | 0.92 | 5.92 | 3.48 × 1023 |
| Muscle | 1.0 | 7.42 | 3.36 × 1023 |
| Bone | 1.85 | 13.8 | 3.00 × 1023 |
Compton Scattering Angle
Scatter angle and energy change are dictated by conservation of energy and momentum. After scattering, the energy is shared between the electron and the scattered photon minus the binding energy of the electron.
Note: the binding energy is often taken to be “0” because the electron is weakly bound and said to be “free.”
![]()
![]()
- E’ is the energy of photon after interaction in MeV
- E0 is the energy of the photon before interaction in MeV
- Φ is the scattering angle of the photon
- 0.511 – rest mass of electron in MeV
- Eelectron is the electron energy after scatter
- Ebinding is the electron binding energy before scatter. Typically taken to be 0.
Key Point: Compton Scattering Angle
- As photon energy increases, the angular scatter distribution becomes more forward peaked.
- Reference angles:
- Forward scatter (0º scatters): The photon retains all of its energy (no interaction)
- Side scatter (90º scatters): The photon retains up to a maximum of 0.511 MeV.
- Back scatter (180º scatters): The photon retains up to a maximum of 0.255 MeV.
Pair Production
In pair production, a photon transitions to an electron/positron pair. The presence of a massive particle is required. This allows for conservation of energy and momentum as the massive particle is able to absorb some recoil energy.
Pair production typically occurs via interaction of a photon and an atomic nucleus.
Triplet production is a special type of pair production which occurs when the massive particle is an electron. Triplet production is less common and requires more energy than pair production.
Requirements
- Energy threshold
- Pair production: 2 × me = 1.022 MeV
- Twice the rest mass of an electron plus a small (typically neglected) additional energy to be transferred to the nucleus.
- Triplet production: 2×me + (3 × 2/3)me = 4me = 2.044 MeV
- Energy to create the rest mass of the electron and positron PLUS each of the three particles must acquire a kinetic energy of about 2/3MeV!
- Pair production: 2 × me = 1.022 MeV
- Occurs near a particle with mass, usually an atomic nucleus
- This is required as the particle must absorb some recoil energy for conservation of both momentum and energy.
Probability of Pair Production
![]()
Key Point: Although the threshold energy for pair production is only 1.022 MeV, it does not become a significant concern in clinical radiation therapy for beams under 10MV.
Photodisintegration
During photodisintegration an atomic nucleus absorbs a high-energy photon, causing the nucleus to decay into its constituent particles.
Decay products commonly include protons, neutrons, alpha particles and other more massive nuclides.
Energy Threshold
Because photodisintegration breaks nuclear bonds, the required minimum energy is in the range of 8-10MeV.
Charged Particle Interactions
| Property | Electrons | Protons |
|---|---|---|
| Path | Many high angle scatters due to low mass | Travels in straighter path due to increased mass |
| Bragg Peak | Not clinically present due to range straggling | Used clinically, requires energy selection or bolus to target desired depth |
| Clinical Energy Range | 6MeV - 22MeV | 6MeV - 230MeV |
General Concepts
Owing to their electric charge, most charge particle interactions are dominated by Coulomb's law. As a result, energy loss occurs continuously, rather than discretely, based on the magnitude of the particles charge and its interaction time (velocity).
![]()
- C is the particles charge
- Thus, alpha particles (charge = 2+) interact much more strongly for the same velocity than do protons or electrons (charge = 1 or 1- respectively).
- v is the particles speed
- Particles with greater speed have less time to interact and thus are able to transfer less energy.
- Changes in energy for relativistic particles changes their mass more than their velocity. Thus while a charged particle is relativistic, its rate of energy loss is roughly independent of velocity.
- This leads to a “Bragg Peak” in which the charged particle gives up most of its energy near the end of its path.
Coulomb's Law
![]()
- ke: Coulomb's constant (9 × 109 N·m2/C2)
- qn: charge n
- r: distance between charges 1 and 2
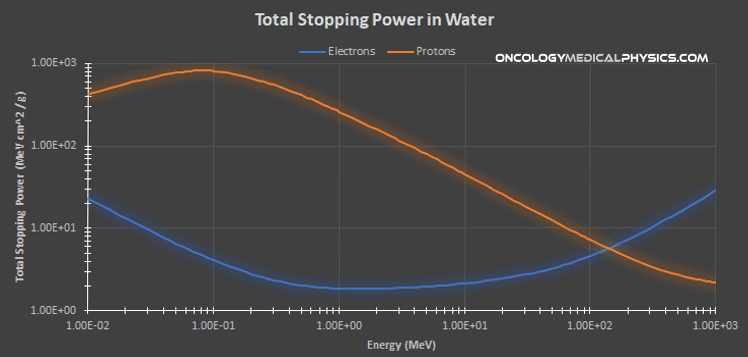
Stopping Power
Stopping power S(E) refers to the energy loss by charged particles per unit path length of a material.
Equation:
![]()
Mass Stopping Power (S/ρ): Stopping power is commonly presented as mass stopping power which is the ratio of stopping power to the material density.
Factors impacting stopping power
Stopping power is a property of the material that the charged particles are passing through.
Energy Dependence:
Stopping power is proportional to the square of the particles charge and inversely proportional the square of the particle's velocity.
![]()
Stopping power tends to vary slowly with energy for relativistic particle energies because of its proportionality to velocity. At lower energies, where velocity varies directly with energy, stopping power varies significantly with energy giving rise to a Bragg peak.
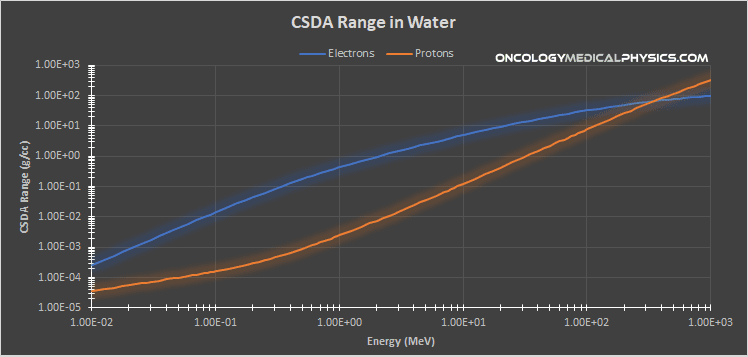
Charged Particle Range
Range (R) is related to stopping power as: ![]()
Continuous Slowing Down Approximation (CSDA)
The range of a charged particle is often computed assuming a continuous set of Coulomb interactions with the medium. This range, referred to as the CSDA range, is based on the average energy loss per unit path length in a given medium.
Impact of Charged Particle Mass
Scatter angle in tissue is greatly impacted by the mass of the charged particles. The mass of a proton is approximately 1,835 times that of an electron (mp = 938MeV, me = 0.511MeV). As a result, protons tend to travel in straighter paths than electrons.
Bragg Peak
Because energy loss by Coulomb interaction is proportional to 1/v2, a large portion of a charged particles energy is lost near the end of its path. This phenomenon results in a significant increase in deposited dose near end of a charged particle's path. This increased dose deposition is known as a Bragg Peak.
Important Points
- Bragg peaks are exploited in proton therapy to improve dose distributions.
- Range straggling and energy straggling reduce the sharpness of a clinical Bragg peak. This is why Bragg peaks are not present in clinical electron beams.
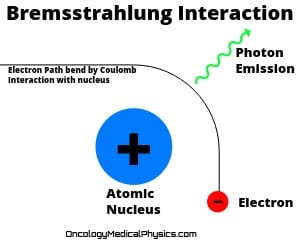
Bremsstrahlung (Braking) Radiation
Bremsstrahlung radiation is electromagnetic radiation produced as a charged particle slows and scatters during interaction with an atomic nucleus.
Bremsstrahlung energy efficiency is the ratio of the output energy emitted as X-rays to input energy deposited by electrons in a linac target. Bremsstrahlung energy efficiency may be approximated as in the below equation where Z is the target atomic number and E is the accelerating energy in volts.
![]()
Note: The above efficiency relationship holds only in the low MV region (<12MV). Source: Khan, F. M. (2010). Physics of X-ray Production. In The Physics of Radiation Therapy (p. 31). Baltimore, MA: Lippincott Williams & Wilkins.
![]()
Clinical Use of Bremsstrahlung Radiation
Bremsstrahlung is used to generate kV imaging X-ray beams as well as high energy MV beams in linear accelerators. This is an extremely inefficient process with only about 1% efficiency for kV (imaging) beams but improves markedly in the MV region with clinical linear accelerators achieving between 30% and 95% efficiency.
Neutron Interactions
Recoil Interactions
- A neutron hits a nucleus and transfers some energy to it. The charged nucleus then produces further ionizations through Coulomb interactions.
- Maximum energy transfer is limited by conservation of charge and momentum.
- Interaction of a hydrogen nucleus (a proton) allows for maximum energy transfer because of their similar masses.
- Interactions with heavy elements result in little energy transfer (think of a ball hitting a wall).
Nuclear Activation
- Neutrons, especially low energy “thermal” neutrons, may also be absorbed by the nucleus. This may produce a spontaneous decay of the nucleus or it could yield a new isotope which may undergo decay at a later time.
- Neutron activation is the process of creating a radioactive isotope through neutron interactions.
- Due to its high hydrogen content, neutron dose to fat is about 20% higher than dose to muscle for the same fluence and energy.
Navigation
Not a Premium Member?
Sign up today to get access to hundreds of ABR style practice questions.