Diagnostic Probabilities

Receiver Operating Characteristics & Bayesian Statistics

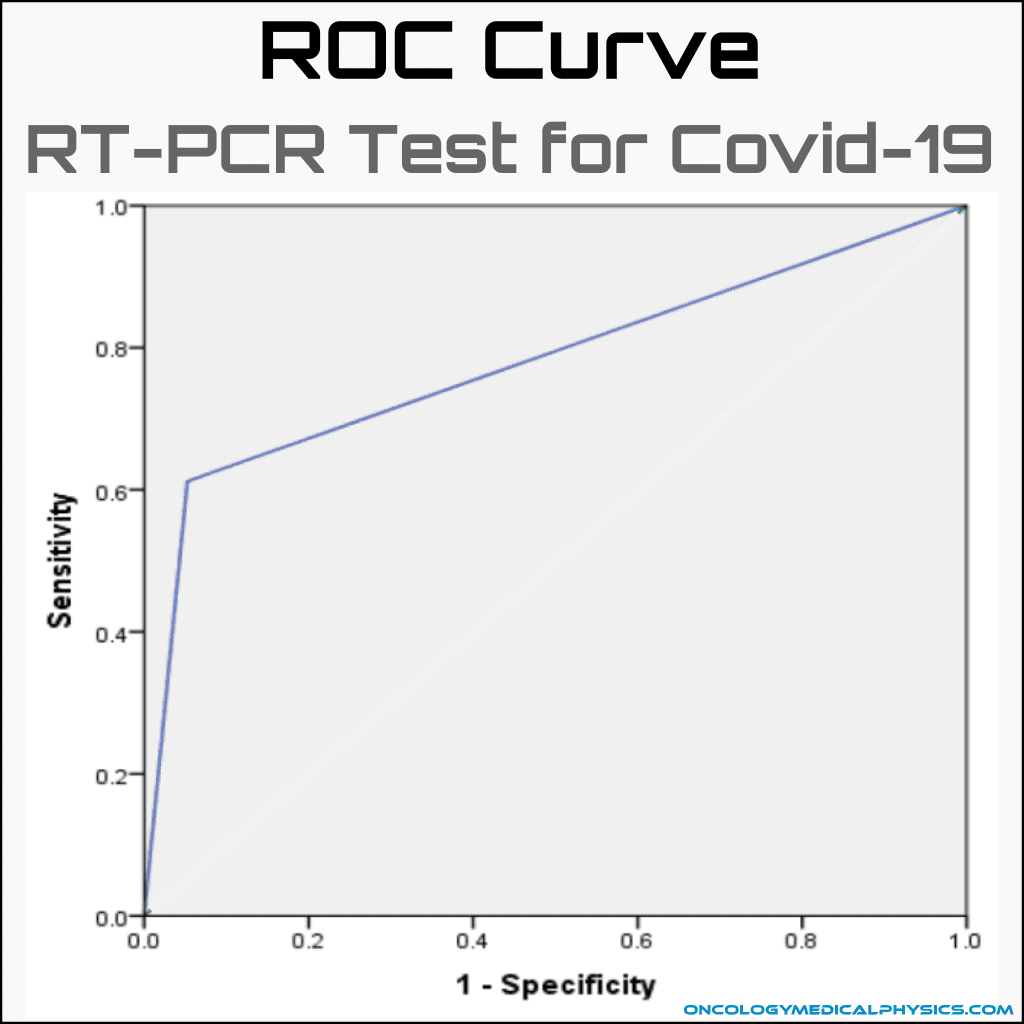
Receiver Operating Characteristic (ROC) Curves

ROC curves plot the probability of correct detection (true positive) as a function of the probability of false detection (false positive). ROC curves are used to determine a detection method’s usefulness.

	Actually Abnormal	Actually Normal
Diagnosed as Abnormal	True Positive (TP)	False Positive (FP)
Diagnosed as Normal	False Negative (FN)	True Negative (TN)

Illustration of diagnostic decision criteria impact on true and false positive rate.

Test Quality Metrics

Area under the curve (AUC): Higher is better; ideal is 1

Sensitivity: True Positive Fraction (TPF)

Specificity: Fraction of normal cases diagnosed correctly

False Positive Fraction (FPF)

Accuracy: Percent of cases correctly diagnosed

Positive Predictive Value (PPV): fraction of positive predictions which are accurate

Negative Predictive Value (NPV): Fraction of negative predictions which are accurate

ROC curve for RT-PCR test detection of COVID-19. Adapted from "Covid-19 Screening by RT-PCR: An Epidological Modelling" by Ali. A. Hasab under CC BY 4.0 license. https://creativecommons.org/licenses/by/4.0/

Bayesian Statistics

Bayes’ theorem: Given the related events A and B, the probability of A given that B is true is equal to the probability of B given that A is true times the probability that A is true divided by the probability that B is true.

Bayes’ theorem, the basis of Bayesian statistics, is finds a variety of uses ranging from assessing the probability that a test subject has a medical condition to spam filtering (external link). In medicine we are most often interested in answering the question “What is the probability that a patient has a disease given that a test yields a positive result.” Understanding Bayesian statistics is especially important for the case of rare diseases as the results can be counter-intuitive.

For example, say that a diagnostic test is known to correctly identify the 99% of all subjects with a given disease and that only 0.1% of the population has that disease. The test in this example also incorrectly yields a positive result for 2% of healthy subjects. What is the probability that a patient who has a positive test result actually has the disease? (Hint: It’s not 99%!)

Bayes’ theorem says that the probability of a subject with a positive test has the disease, P(A|B), is dependent not only on the probability that a diseased subject will be correctly identified, P(B|A), but also on the probability that the subject has the disease in absence of the test, P(A), and the total probability of a positive test, P(B).

Using the notation of an ROC diagram, Bayes’ theorem can then be rewritten as:

If no prior tests have been performed, the probability that the subject has the disease in absence of the test [P(A)] is taken as the incidence rate of the disease in the population of interest. In the above example this would yield a probability that the patient actually has the disease as only 4.7%!

If the same test is run again on the same subject and another positive result is found, the prior probability, P(A), is now taken to be 4.7%. This yields a probability that the subject has the disease of 70.9%.