Detection Efficiency and Dead Time
Making Accurate Activity Measurements
Knowledge of which radionuclide is present is a prerequisite for determining the activity of a source based on counting measurements of its decay products. This is because some radioactive decay events yield more than one decay product per decay. For example: 94.6% of Cs-137 decays will yield a single gamma-ray while 99.88% of Co-60 decays will yield two gamma-rays. Mistaking gamma-ray detections arising from Co-60 for gamma-ray detections arising from Cs-137 would result in an error of measured activity by about a factor of two.
Once radionuclide is determined, determining the source activity is simply a matter of measuring how many particles are emitted per unit of time. Because counting experiments occur over a finite time, counting statistics (internal link) are necessary to analyze the measured data. Additionally, knowledge about the detection efficiency and dead time of the measurement system is required to correct for unmeasured decay events.
Detection Efficiency
Detector efficiency (ε) is defined as the radio of counts recorded to total number of particles emitted from a radiation source. Detector efficiency impacted by geometric efficiency, intrinsic efficiency, and detector dead-time.
![]()
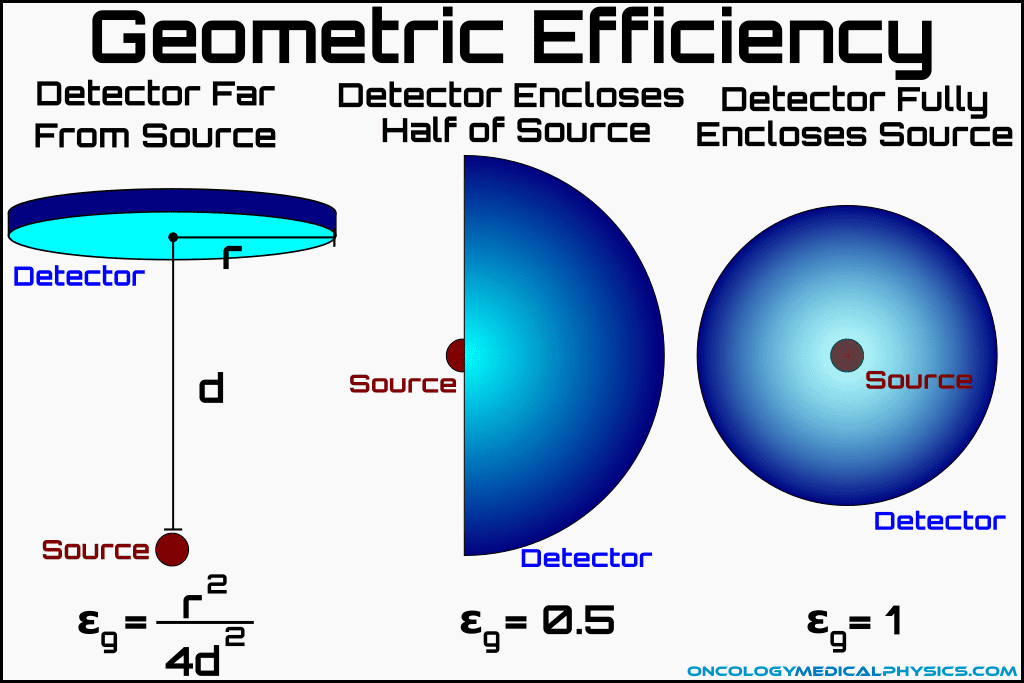
Geometric Efficiency
Ignoring self-attenuation (attenuation of radiation by the radiation source itself), radiation emissions occur isotropically. Therefore, geometric efficiency is approximately equal to the area of the detector entrance divided by the surface area of a sphere with a radius equal to the source-to-detector distance.
![]()
- r is the detector radius
- d is the source-to-detector distance
The above equation is valid only when the source may be approximated as a point, the detector surface is a circle oriented to face the source, and the distance between the source and detector is much greater than the detector radius. If these assumptions are not true, geometric efficiency can be calculated by computing the solid angle (in steradians) of the detector using the below equation.
![]()
- Ω is the solid angle subtended by the detector in units of steradians
Intrinsic Efficiency
Intrinsic efficiency is the ratio of the number of counts recorded by a detector to the total number of particles incident on the detector. Intrinsic efficiency is influenced both by the properties of the detector (density, charge collection efficiency, detector attenuation, etc.) and the incident particles (charge, mass, energy, etc).
![]()
Dead Time
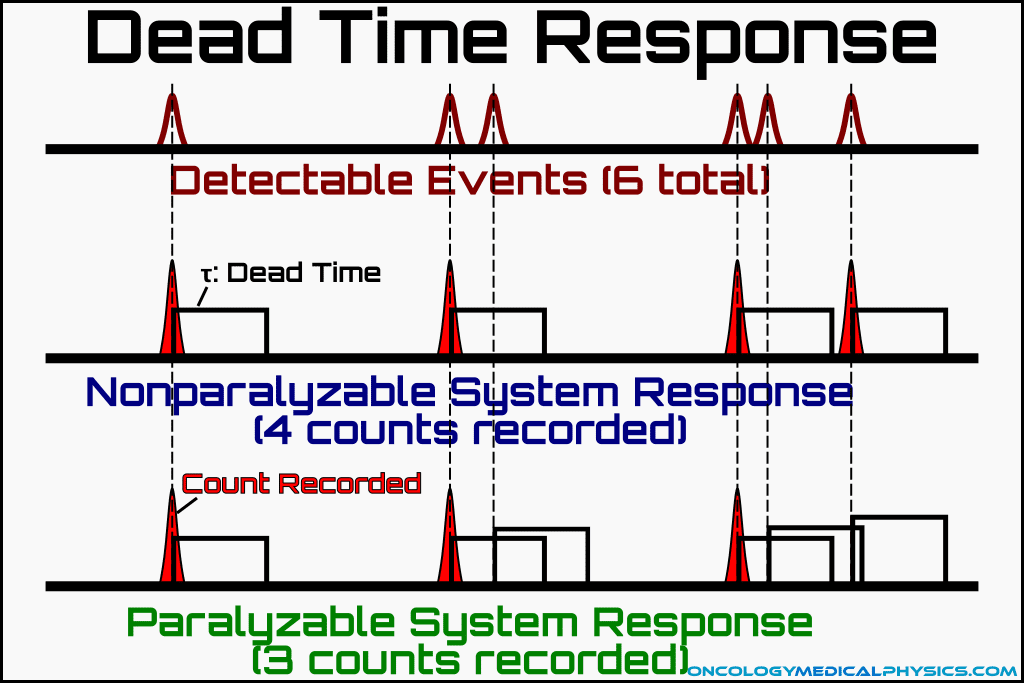
Counting detector systems typically require a minimum amount of time between counts that must occur for the counts to be recorded separately. This minimum time between events is known as dead time. Because radioactive decay is a temporally random process, dead time will result in some counting efficiency loss even at low rates of decay. The fraction of counts lost to dead time will depend on:
- Length of post count dead time (τ)
- The rate of countable events at the detector
- Whether the detector is a paralyzable or nonparalyzable
Paralyzable Counting Systems
Paralyzable counting systems are those in which events occurring during a previous event’s dead time, increase the length of dead time but remain uncounted.
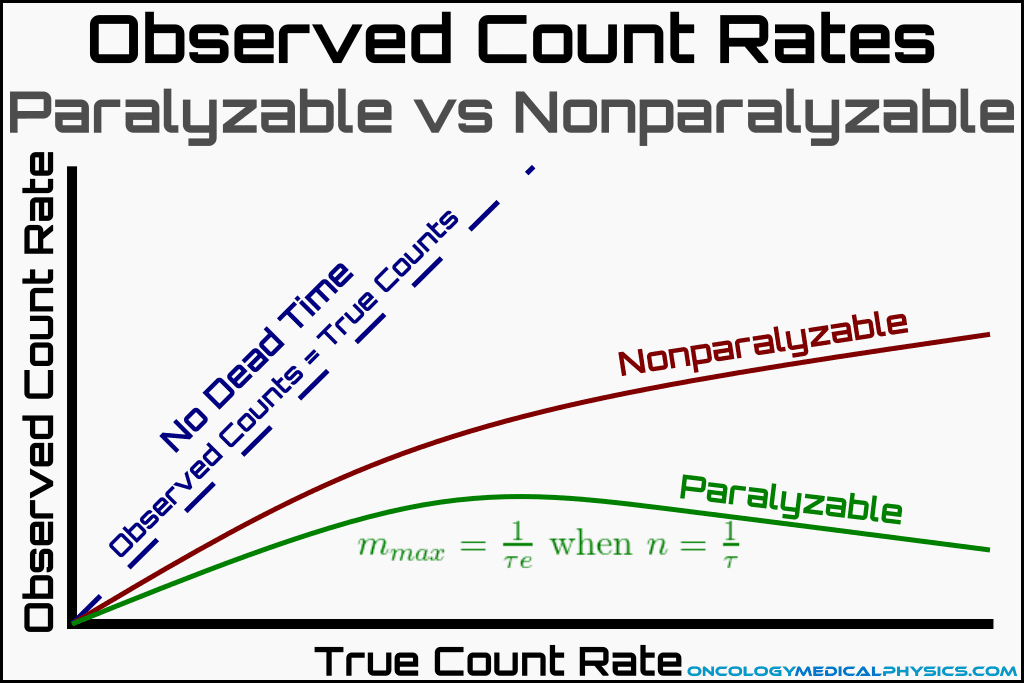
The relationship between measured count rate (m) and true count rate (n) for a paralyzable system are given by:
![]()
For a paralyzable counting system, maximum observed count rate is determined by the dead time and occurs when the true count rate = 1/dead time.
![]()
Nonparalyzable Counting Systems
Nonparalyzable counting systems are those in which events ocurring during a previous event’s dead time do not add additional dead time and are not counted.
The relationship between measured count rate (m) and true count rate (n) for a nonparalyzable system are given by:
![]()
For a nonparalyzable counting system, there is no maximum observed count rate but the counting efficiency continues to decrease with increased true count rate.
Navigation
Not a Premium Member?
Sign up today to get access to hundreds of ABR style practice questions.