High Dose Rate Brachytherapy (HDR)
Overview
High dose rate (HDR) brachytherapy is defined as any brachytherapy procedure which uses a source with a dose rate of 20cGy/min (12 Gy/hour) or higher. In practice, the initial dose rate of a 10Ci Ir-192 source at 1cm is approximately 7.5Gy/minute.
Advantages and Disadvantages of HDR
Advantages
Optimization
Once the treatment catheters are in place, the patient may be imaged and a plan may be generated to optimize dose distribution. Inverse planning is fast due to the lower complexity of HDR plans, in which dwell times are the primary variable, compared to external beam treatments.
Immobilization
The shorter treatment times allow for patient immobilization which would be impractical or impossible with an LDR source. This decreases uncertainty in a dwell position.
Implant Position Stability
All implanted devices move as a result of internal anatomical motion. Because HDR catheters are in the patient’s body for less time, their dose distribution may be more localized.
Reduced Normal Tissue Dose
Organs at risk may be temporarily displaced during treatment. This is especially true for gynecologic and oral treatments but not usually for intraluminal treatments.
Outpatient Treatments
This improves patient comfort and health as the patient maintains a sense of freedom. Further, outpatient treatments are less costly to the patient.
Smaller Source, Less Discomfort
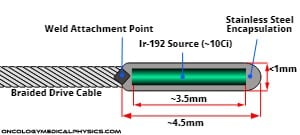
Typical HDR sources have a diameter of 1mm or less meaning compared with an LDR radium needle which may 1.65-2mm in diameter.
Fewer Delays
Treatments are readily adapted to circumstances and may be easily replanned without need to acquire new sources.
Intraoperative Procedures (IORT)
The high dose rate and low energy of Ir-192 makes it a good choice for IORT procedures.
Radiation Worker and Public Safety
Use of a remote afterloader means that staff is never inside the room while the source is unshielded. Further, since the treatments last from 5-30 minutes, the source never leaves the shielded treatment room.
Disadvantages
Reduced Therapeutic Ratios
Radiobiology predict that, for the same amount of damage to tumor cells, HDR will be more damaging to normal cells.
Increased Impact of Errors
Because of the reduced time of treatment, any error in delivery time will be more damaging than for LDR.
Afterloader Failures
The high dose rate means that a failure of the afterloader to retract the source will result in large doses to the patient and staff responsible for retrieving the source.
Require Greater Clinical Resources
The afterloader itself may cost as much as $1,000,000 and requires quarterly source changes. Greater staffing is also needed as the treatments progress from placement to planning to treatment in necessarily quick succession.
Remote Afterloaders
A remote afterloader (RAL), commonly referred to simply as an afterloader, is a motor driven system that transports a radioactive source for a shielded internal safe to a series of predetermined positions. Transfer tubes connect the afterloader to applicator catheters within the patient. The afterloader is then preprogrammed to send the source to specified locations for set amounts of time, referred to as dwell times.
Key Point: An HDR afterloader will typically have an initial source strength of around 10Ci which, for Ir-192 sources, equates to an Air Kerma Strength of approximately 40,820U. This means that, by the TG-43 formalism, the initial dose rate to water at 1cm is 7.6Gy/min!
Afterloader Design Features
Dummy Source/Check Cable
An non-radioactive duplicate of the source cable which is used to test channels, transfer tubes, and applicators for obstructions prior to sending the source cable. The check source will typically extend 2-5mm beyond the expected length of the source cable.
Emergency Retraction Motor
In fault conditions, a second source retraction motor may be engaged. This motor is typically a high-torque direct current motor. Emergency retraction motor should be tested as part of daily quality assurance.
Emergency Crank
An emergency crank allows for source retraction in event that both the primary and emergency motor fails. Since the emergency crank is on the RAL, its use requires staff to enter the treatment room with the source extended.
Source Cable
The source, typically Ir-192, is controlled by a thin metal cable. The source is typically 3-5mm long and <1mm thick. Note that the “cable length” is typically defined as the distance to the middle of the source rather than the end of the source!
HDR Sources
Iridium-192 is the most commonly used HDR source because of its high specific activity allowing for high dose rates from a small source. Further, the low energy of 192Ir (average 380keV) aids in rapid dose fall off and more conformal dose distributions. Because of its short half-life (73.83 days), Iridium-192 sources must be changed every 3-4 months and loose ~1% activity per day.
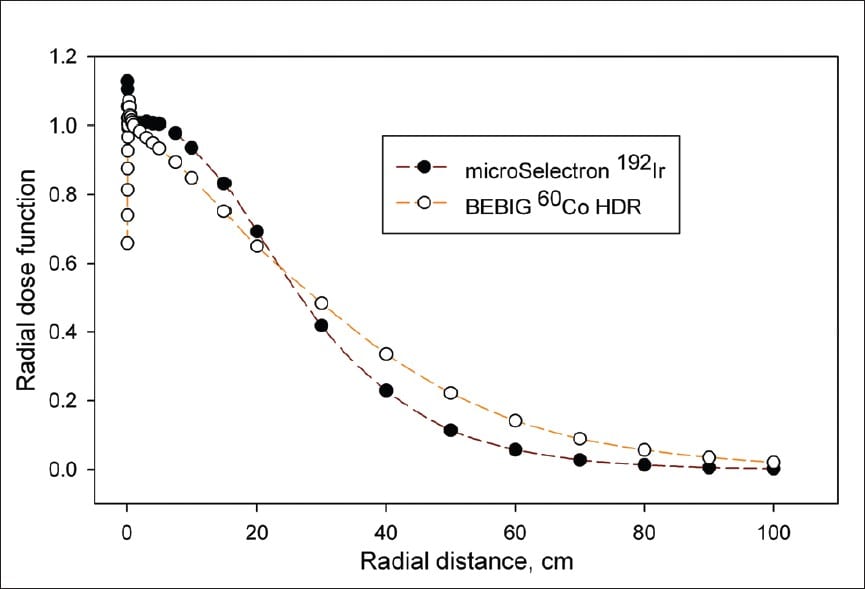
Cobalt-60 is less common but has the advantage of a longer half life (5.3 years) than 192Ir which extends the time between source changes to approximately every 5 years. Lower specific activity of Cobalt units necessitates larger source size for the same activity and dose rate. 60Co has an average energy of energy of 1.25Mev which is significantly greater than 192Ir making for a lower rate of dose fall off (note that dose fall off is still good as its dominated by the inverse square law).
Ytterbium-169 is a radionuclide that is gaining interest because of its very high specific activity and very low energy spectrum. It has a half life of 32.03 days. 169Yb decays via electron capture yielding an average photon energy of 93keV. The low energy also introduces the possibility of directionally shielding sources or applicators.
Pulsed Dose Rate (PDR) Brachytherapy
Pulsed dose rate brachytherapy is a technique designed to produce therapeutic ratios similar to LDR treatments using HDR equipment and sources. In a PDR treatement, the applicator is installed in the patient for approximately 24 hours. During that time, the HDR source will periodically (every hour is common) extend into the treatment positions and deliver some dose. This technique was popular at the onset of high dose rate brachytherapy because of its similarity to low dose rate brachytherapy. The technique is not common today because of the logistical and safety issues of having an afterloader attached to a patient and in use for such a long time.
Navigation
Not a Premium Member?
Sign up today to get access to hundreds of ABR style practice questions.