Brachytherapy Dosimetry
Units
Becquerel (Bq): A measure of source activity defined as 1 disintegration per second.
Curie (Ci): A historical measure of activity defined as approximately the activity of 1 gram of Radium-226.
![]()
Exposure rate constant ![]() : exposure per hour (R/h) at 1cm distance from a 1mCi point source. Units:
: exposure per hour (R/h) at 1cm distance from a 1mCi point source. Units: ![]()
mg-Radium Equivalent: a historical unit used to allow convenient conversion from Ra-226 source strength and the strength of a radionuclide. ![]()
![]()
Air Kerma Strength (SK): As defined in TG-43U1: "Air-Kerma Strength (SK) is the air-kerma rate \(\dot{K}_{\delta}(d)\), in vacuo, due to photons of energy greater than δ at a distance d, multiplied by the square of this distance, d2." Units: U. 1U = 1\(\frac{\mu Gy \ m^2}{hr}\) = 1\(\frac{cGy \ cm^2}{hr}\)

- \(\dot{K}_{\delta}(d)\) denotes the air kerma rate at point d for photons with energy greater than δ.
- Measured in vacuo, meaning corrected for all photon attenuation and scattering due to air as well as surrounding objects
- δ is typically taken to be 5keV
- d denotes the the point of measurement
mg-hour: Milligram hours was used as a measure of total exposure/dose when using Radium-226 seeds. It is defined as the product mass of Radium-226 and irradiation time.
Total Reference Air Kerma (TRAK): an analogous quantity to mg-hours defines as the product of Air-kerma strength and time.
\begin{equation} TRAK = \sum{t \cdot S_{k}} \end{equation}
Common Radiation Sources
| Nuclide | Half-life | Photon Energy (MeV) | HVL (mm Lead) | Exposure Rate Constant (R-cm2/mCi-hr) |
|---|---|---|---|---|
| 192Ir | 73.8 days | 0.38 average | 2.5 | 4.69 |
| 226Ra | 1,600 years | 0.83 average | 12.0 | 8.25 |
| 222Rn | 3.83 days | 0.83 average | 12.0 | 10.15 |
| 60Co | 5.26 years | 1.17, 1.33 | 11.0 | 13.07 |
| 137Cs | 30.0 years | 0.662 | 5.5 | 3.26 |
| 198Au | 2.7 days | 0.412 | 2.5 | 2.38 |
| 125I | 59.4 days | 0.028 average | 0.025 | 1.46 |
| 103Pd | 17.0 days | 0.021 average | 0.008 | 1.48 |
NIST Photon Source Calibration
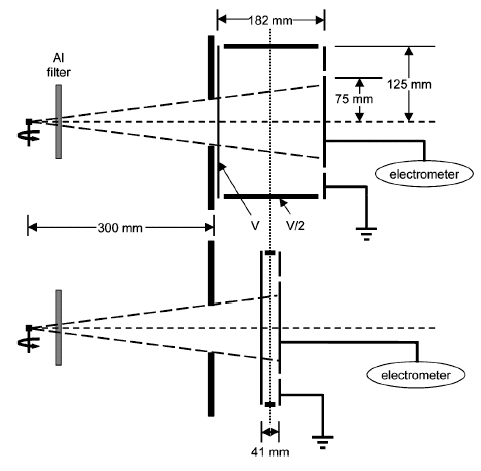
The Wide Angle Free-Air Chamber (WAFAC) is the current NIST standard instrument for the characterization of brachytherapy sources. The WAFAC is a cylindrical chamber with circular symmetry about the beam axis.
WAFAC Components
- Beam enters the dosimeter through a 8cm circular aperture located 30cm from the source.
- An aluminum filter is placed between the source and the dosimeter eliminate Ti K-shell X-rays arising from source encapsulation.
- Varying the active volume of the dosimeter allows for correction of measurement induced effects such as those induced by the aluminized-PET electrodes.
NIST Beta Source Calibration
NIST uses an extrapolation chamber to determine the zero gap measure (dose at window surface).
- Dose is specified to water.
- For intravascular sources, dose is specified to a depth of 2mm.
- For ophthalmic sources (sources for ocular therapy), dose is specified to surface.
Source Dosimetry (AAPM TG-43)
Overview
AAPM TG-43: Dosimetry of Interstitial Brachytherapy Sources was published in 1995 to standardize brachytherapy source strength and dose rate calculations. The report also gave consensus data for several sources, discussed uncertainty, and provided information on the relationship between TG-43 quantities on other formalisms.
TG-43 was updated in 2004 with the publication of Update of AAPM Task Group No. 43 Report: A revised AAPM protocol for brachytherapy dose calculations which is typically referred to as AAPM TG-43U1. TG-43U1 updated some definitions (outlined below), corrected minor inconsistencies, and provided additional consensus data sets.
In 2007 Supplement to the 2004 update of the AAPM Task Group No. 43 Report was released. This supplement provided additional consensus source data sets.
Changes between TG-43 and TG-43U1
- Revised definition of air-kerma strength
- Included cutoff energy and specified in vacuo measurement
- Elimination of apparent activity for specification of source strength
- Replaces anisotropy constant with the distance-dependent 1D anisotropy function.
- Provides guidance on extrapolating TG-43 parameters to longer and shorter distances
- Corrects some errors and omissions
2D Formalism
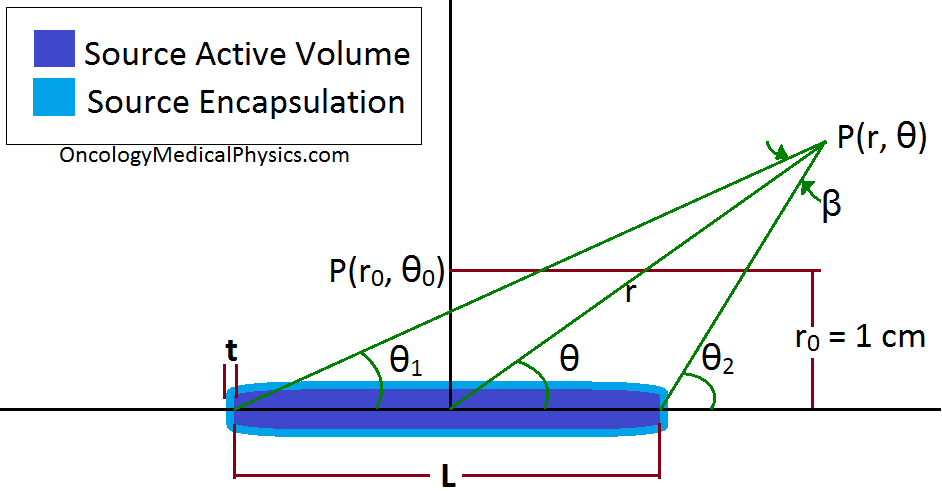
The general 2 dimensional equation for dose rate (D˙) is given below:
![]()
- r denotes the distance in centimeters from the center of the source
- θ denotes the polar angle between the point of interest and the longitudinal axis of the source
- The subscript “0” (as in r0 or θ0) denotes measurements to the reference point which is specified at 1cm from the center of the course at an angle of 90 degrees relative to the source’s longitudinal axis
- The subscript “L” (as in GL or gL) denotes that the quantities are for a line source.
Air-Kerma Strength
As defined in TG-43U1: "Air-Kerma Strength (SK) is the air-kerma rate \(\dot{K}_{\delta}(d)\), in vacuo, due to photons of energy greater than δ at a distance d, multiplied by the square of this distance, d2."
![]()
- SK is the Air-Kerma Strength
- A typical value to a 10Ci Ir-192 HDR source is about 40,000U.
- \(\dot{K}_{\delta}(d)\) denotes the air kerma rate at point d for photons with energy greater than δ.
- Measured in vacuo, meaning corrected for all photon attenuation and scattering due to air as well as surrounding objects.
- δ is typically taken to be 5keV.
- d denotes the the point of measurement
- Units: \(\frac{\mu Gy \ m^2}{h}\), \(\frac{cGy \ cm^2}{h}\)
- The unit "U" is defined as 1U = 1\(\frac{\mu Gy \ m^2}{h}\) = 1\(\frac{cGy \ cm^2}{h}\)
Determining Air-Kerma Strength from Apparent Activity (Aapp)
![]()
- Aapp is apparent activity in (mCi).
- W/e = 33.97 (J/C) = 0.876 (cGy/R) for dry air.
- Γ𝛿 is the exposure rate constant. Nominally 4.69 (R cm2 / mCi hr) for Ir-192.
Differences in Air-Kerma Strength between TG-43 and TG-43U1
- The cutoff energy, δ, was not included in either the original TG-32 nor the TG-43 definition of Air-Kerma Strength. However, it was included in TG-43U1 because inclusion of low energy photons greatly increased measurement uncertainty while invaliding some theoretical underpinnings of dosimetry models.
- Prevailing conditions (i.e. in vacuo) are explicitly stated in TG-43U1
Dose Rate Constant
The dose-rate constant, Λ, is the ratio of dose rate at the reference point, \(\dot{D}(r_0, \theta_0)\), to the air-kerma strength, SK, as in the below equation:
![]()
- Λ is influenced both by radionuclide and the design of the source model.
- Sometimes denoted "ΛnnD,PqqS" (I.e. Λ97D,N99S)
- D denotes reference dose rate
- nn denotes the year that the reference dose rate was published
- P denotes the provider of the source strength standard (N for NIST, T for Theragenic Corporation)
- qq denotes the year the source strength standard was implemented
- S denotes the word "standard"
- Units: \(\frac{cGy}{h \ U} = cm^{-2}\)
- Common source values:
- VariSource (Ir-192): Λ = 1.044 \(\frac{cGy}{h \ U}\)
- MicroSelectron (Ir-192): Λ = 1.115 \(\frac{cGy}{h \ U}\)
- Flexitron (Ir-192): Λ = 1.112 \(\frac{cGy}{h \ U}\)
Geometry Function
The geometry function, G, accounts for the inverse square law. Geometry functions for point and line sources, denoted with the P or L subscript respectively, are given in the below equations:
![]()

- Accounts only for inverse square law, neglecting scatter and attenuation
- β is the angle, in radians, subtended by the line source at the calculation point P(r, θ)
- TG-43 and TG-43U1 recommend using the line source approximation, GL, for all 2D dose calculations.
- 1D dose calculations may use either point or line source approximations. Use of the line source approximation is preferred but most planning systems use the point source approximation.
Effective Length
For sources containing multiple, uniformly spaced radioactive components effective length, the below equation should be used.

- N is the number of discrete radioactive pellets.
- ΔS is the nominal center-to-center spacing of the radioactive pellets.
- Lcap is the physical length of the source capsule. (Not defined in TG-43, used here for brevity.)
- Pdist is the distal aspect of the source. (Not defined in TG-43, used here for brevity.)
- Pprox is the proximal aspect of the source. (Not defined in TG-43, used here for brevity.)
Radial Dose Function
Accounts for dose fall off in the transverse plane due to photon scattering and attenuation. If does not include inverse square fall off which is handled by the Geometry Function.
![]()
- X (as in gX, LX,and GX) is a placeholder for point source, P, or line source, L.
- gX is provided in tabular form fitting a 5th order polynomial to within 2%
- \(g_x(r) = a_0 + a_1 r + a_2 r^2 + a_3 r^3 + a_4 r^4 + a_5 r^5\)
- g(1cm) = 1 by definition
- For an Ir-192 HDR source, g(r) increases to a maximum value of about 1.005 at a depth of approximately 3cm. After that point g(r) decreases to around 0.7 at 20cm.
2D Anisotropy Function
The 2D Anisotropy Function expresses the variation in dose with polar angle relative to the transverse plane.
![]()
F(r, θ) decreases as
- r decreases
- θ approaches 0° or 180° (minimum values may be as low as 0.65 to 0.45 for an HDR source)
- Encapsulation thickness increases
- Photon energy decreases
1D Formalism
Although it is only an approximation of the 2D procedure, the 1D dose rate formalism, below, simplifies source localization procedures because information about source orientation is not needed.
![]()
- It is recommended that the line source approximation be used for the geometry function GX.
1D Anisotropy Function
The 1D anisotropy function, φan, is the ratio of dose rate at a distance r, averaged with respect to solid angle, to dose rate on the transverse axis at the same distance.
![]()
- Typically φan < 1.
- The 1D anisotropy function may be appropriate for LDR setups with many seeds of unknown orientations. (E.g. LDR prostate brachytherapy).
Anisotropy Constant (eliminated in TG-43U1)
In TG-43, an anisotropy constant \(\bar{\phi}_{an}\) was allowed rather than a distance dependent function. However, this constant was eliminated in TG-43U1.
Navigation
Not a Premium Member?
Sign up today to get access to hundreds of ABR style practice questions.