Accuracy, Precision, and Error
Understanding Error and Measurement Confidence
Definitions
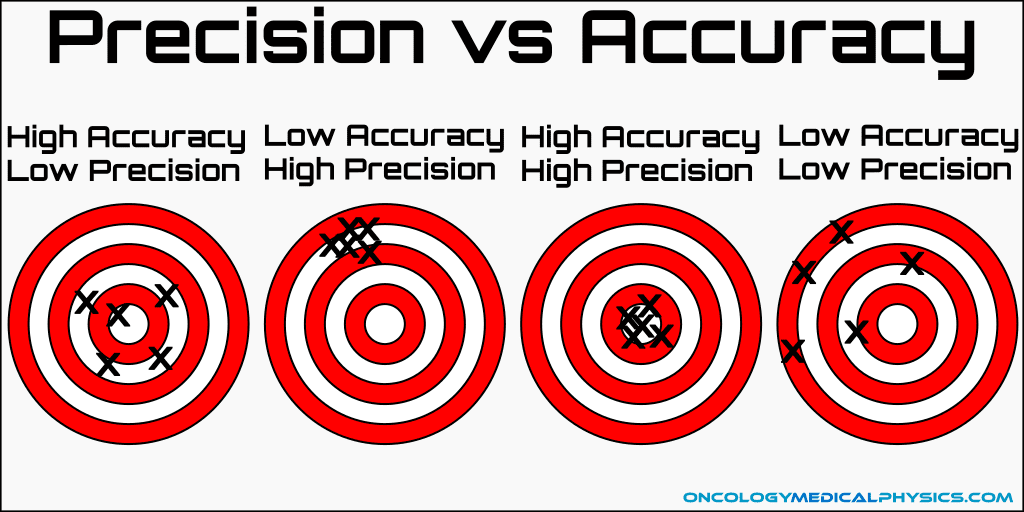
Accuracy describes how closely a given measurement matches the true value.
Precision describes the ranges of measured values and is closely related to deviation and standard deviation.
Measurement error is the difference between a measured value, derived from the sample, and the true population value. Measurement error is a metric of accuracy and is usually not precisely knowable.
Measurement uncertainty is an interval around that a measured value such that any repetition of the measurement will produce a new result that lies within this interval. Measurement uncertainty is a metric of precision and can be quantified.
A confidence interval is used to quantify measurement uncertainty. Confidence intervals express the percent certainty that the true value lies within a given range of values.
Example:
A measurement of π yields a 95% confidence interval of π = 3.00 ± 0.5. This indicates that the measurement is 95% certain that the true value of π is between 2.5 and 3.5. Taking the true value of π as π=3.14, we would have a measurement error of 0.14.
Sources of Error
Random Errors
As the name suggests, random errors are random. They cannot be predicted but generally represent themselves as fluctuations centered about the mean.
Common Statistical Errors
Statistical Error: Statistical Error is fundamental to counting experiments due to the familiar relationship between standard deviation and mean value:
![]()
Electronic Noise: Electronic noise is present in measurements involving analog electronic measurements. Critically, the noise will be present even if an analog signal is converted to digital prior to displaying the result.
Daily Patient Alignment Errors: In external beam radiotherapy, daily variation in patient positioning is a source of random errors in the delivered dose distribution.
Systematic Errors
Systematic errors are errors which consistently influence a measurement in a given direction. Systematic errors are most commonly either measurement offsets (E.g. a ruler always measures 1mm long) or a multiplication error (E.g. a ruler that measures 1.1 times the true length). Unlike random errors, systematic errors can be accounted for using a calibration factor.
Common Systematic Errors
Measurement Device Errors: Measurement device errors result from incorrect calibration of the device used to take a measurement.
Atmospherically Induced Errors: Atmospherically induced errors are commonly found in radiation measurement applications where the response of the measurement device is dependent upon temperature or pressure.
Patient Simulation Errors: In external beam radiotherapy, errors in patient or organ positioning that are present during CT simulation will be propagated as systematic error throughout the entire treatment. For example, a CT image which places a tumor 1mm below the true tumor location would yield a treatment plan which delivers dose consistently 1mm below the true tumor.
Combining Sources of Error (Error Propagation)
Multiple sources of error are present in all real world measurements. These sources of error must be combined, propagated, to assess the total error in the measurement. Error propagation is accomplished by taking the partial derivative of the equation defining the final value as below.
![]()
- C is the combined measurement
- x, y, and z are individual components of the measurement
- σ is standard deviation
Addition and Subtraction
For equations of the forms
![]()
The partial derivative with respect to x and y are
![]()
Which result in the combined error equation of
![]()
Multiplication by a Constant
For equations of the form
![]()
The partial derivative with respect to x is
![]()
Which result in the combined error equation of
![]()
Division by a Constant
For equations of the form
![]()
The partial derivative with respect to x is
![]()
Which result in the combined error equation of
![]()
Multiplication by a Variable
For equations of the form
![]()
The partial derivative with respect to x and y is
![]()
Which result in the combined error equation of
![]()
Division by a Variable
For equations of the form
![]()
The partial derivative with respect to x and y is
![]()
Which result in the combined error equation of
![]()
Average of Multiple Independent Measurements
![]()
Where N is the number of independent measurements.
Navigation
Not a Member?
Sign up today to get access to hundreds of ABR style practice questions.